15 Lecture 6: The Multiple Regression Model II

Slides

• 5 The Simple Regression Model (link)

15.1 Introduction

## 
## Attaching package: 'ggpubr'

## The following objects are masked from 'package:tidylog':
## 
##     group_by, mutate

We continue studying the simple regression model.

Figure 15.1: Slides for 7 The Multiple Regression Model.

15.2 Vignette 6.1

Once again, let’s simulate some data. Maybe we are interested in urban and rural towns (70% are urban) :

df <- tibble(urban = sample(c(0,1),500,replace=T,prob=c(.3,.7))) %>%
  ## Urban towns spend, on average, $3 million more on wages than rural towns
  mutate(expen_wages = 3*urban+runif(500,min=0,max=4)) %>%
  ## Urban towns are also have greater incomes (e.g., from taxes), but these are reduced by their high wage expenditures:
  mutate(log_income = 1 + 2*urban - .3*expen_wages + rnorm(500,mean=2)) ## <- Population Eq.

Now we can estimate the effect of wage expenditure on income:

model_a <- lm(log_income ~ expen_wages, data = df) 
summary(model_a) 

## 
## Call:
## lm(formula = log_income ~ expen_wages, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.7311 -0.8162 -0.0090  0.8356  3.7481 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.77873    0.12406  22.399  < 2e-16 ***
## expen_wages  0.07650    0.02735   2.797  0.00536 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.161 on 498 degrees of freedom
## Multiple R-squared:  0.01547,    Adjusted R-squared:  0.01349 
## F-statistic: 7.823 on 1 and 498 DF,  p-value: 0.005358

Wait what? (Interpret a log ~ level)

15.3 Vignette 6.2

Let’s see… How can we remove everything from wages that is explained by urban? How can we remove everything from income that is explained by urban?

df %>% group_by(urban) %>%
  summarise(income_urb= mean(log_income)) 

## summarise: now 2 rows and 2 columns, ungrouped

## # A tibble: 2 × 2
##   urban income_urb
##   <dbl>      <dbl>
## 1     0       2.40
## 2     1       3.41

df %>% group_by(urban) %>% 
  summarise(expen_wages_urb = mean(expen_wages))

## summarise: now 2 rows and 2 columns, ungrouped

## # A tibble: 2 × 2
##   urban expen_wages_urb
##   <dbl>           <dbl>
## 1     0            1.89
## 2     1            5.13

The difference between what is explained by urban of income/expendinture (mean) and the observed value of income/expenditure is…

df <- df %>% group_by(urban) %>%
  mutate(log_income_residual = log_income - mean(log_income),
         expen_wages_residual = expen_wages - mean(expen_wages)) %>%
  ungroup()

## ungroup: no grouping variables remain

The residual… what is not explained by urban!!

model_b <- lm(log_income_residual ~ expen_wages_residual, data = df) 
summary(model_b) ### CLOSER!

## 
## Call:
## lm(formula = log_income_residual ~ expen_wages_residual, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.4334 -0.6873  0.0127  0.6745  3.2361 
## 
## Coefficients:
##                        Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          -1.951e-16  4.491e-02   0.000        1    
## expen_wages_residual -3.206e-01  3.872e-02  -8.279 1.15e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.004 on 498 degrees of freedom
## Multiple R-squared:  0.121,  Adjusted R-squared:  0.1192 
## F-statistic: 68.55 on 1 and 498 DF,  p-value: 1.148e-15

Let’s plot:

A <- ggplot(df, aes(x=expen_wages,y=log_income)) +
  geom_point() +
  labs(title = "0. Relation between wages and income. Beta = 0.13") +
  geom_smooth(method = "lm") +
  xlim(c(-3,7)) + ylim(c(-3,6))
A

## `geom_smooth()` using formula = 'y ~ x'

B <- ggplot(df, aes(x=expen_wages,y=log_income,color = factor(urban))) +
  geom_point() +
  labs(title = "1. Relation between wages and income divided by urban.") +
  xlim(c(-3,7)) + ylim(c(-3,6))
B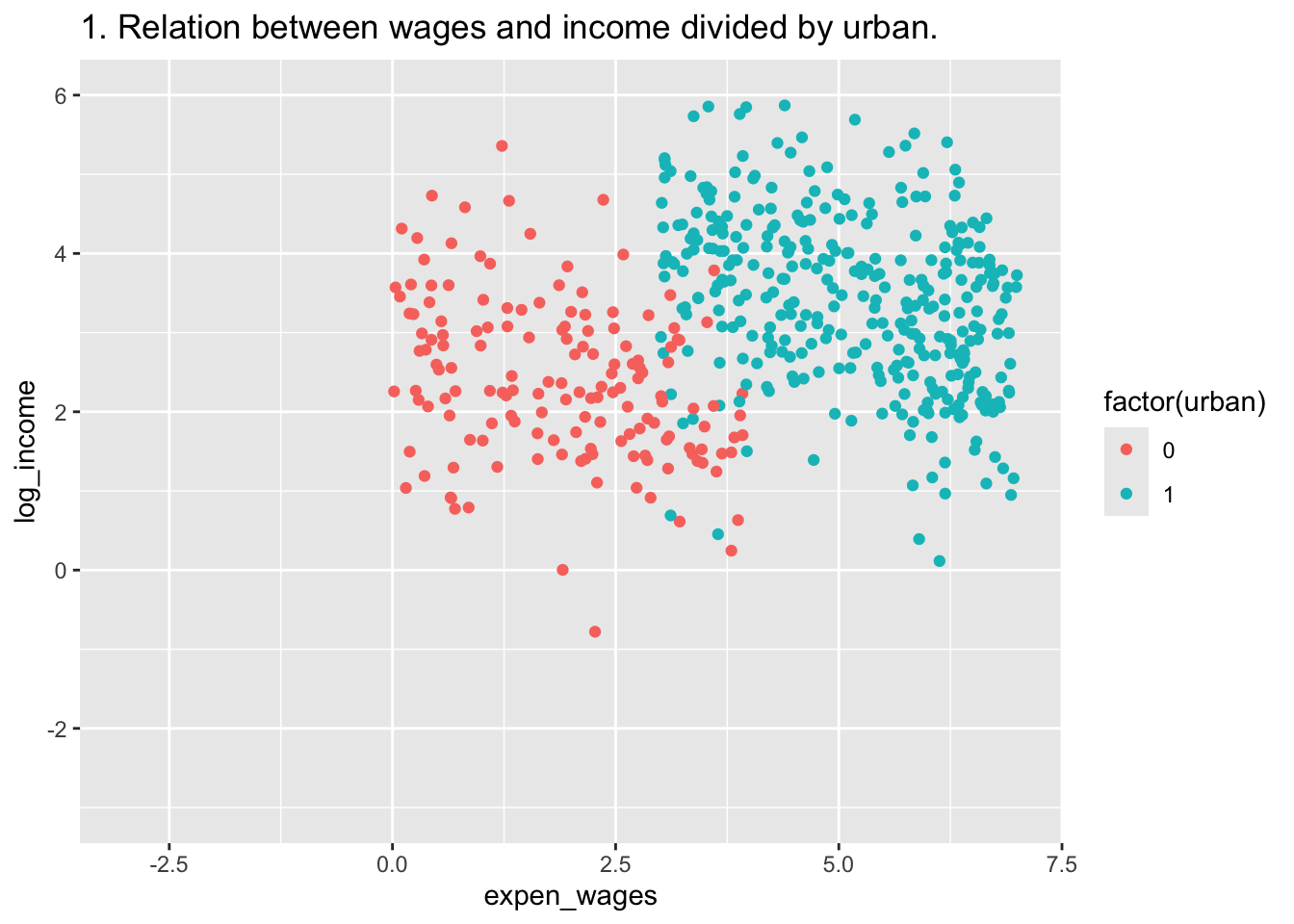

C <- ggplot(df, aes(x=expen_wages_residual,y=log_income,color = factor(urban))) +
  geom_point() +
  labs(title = "2. We remove the difference of wages explained by urban.")+
  xlim(c(-3,7)) + ylim(c(-3,6))
C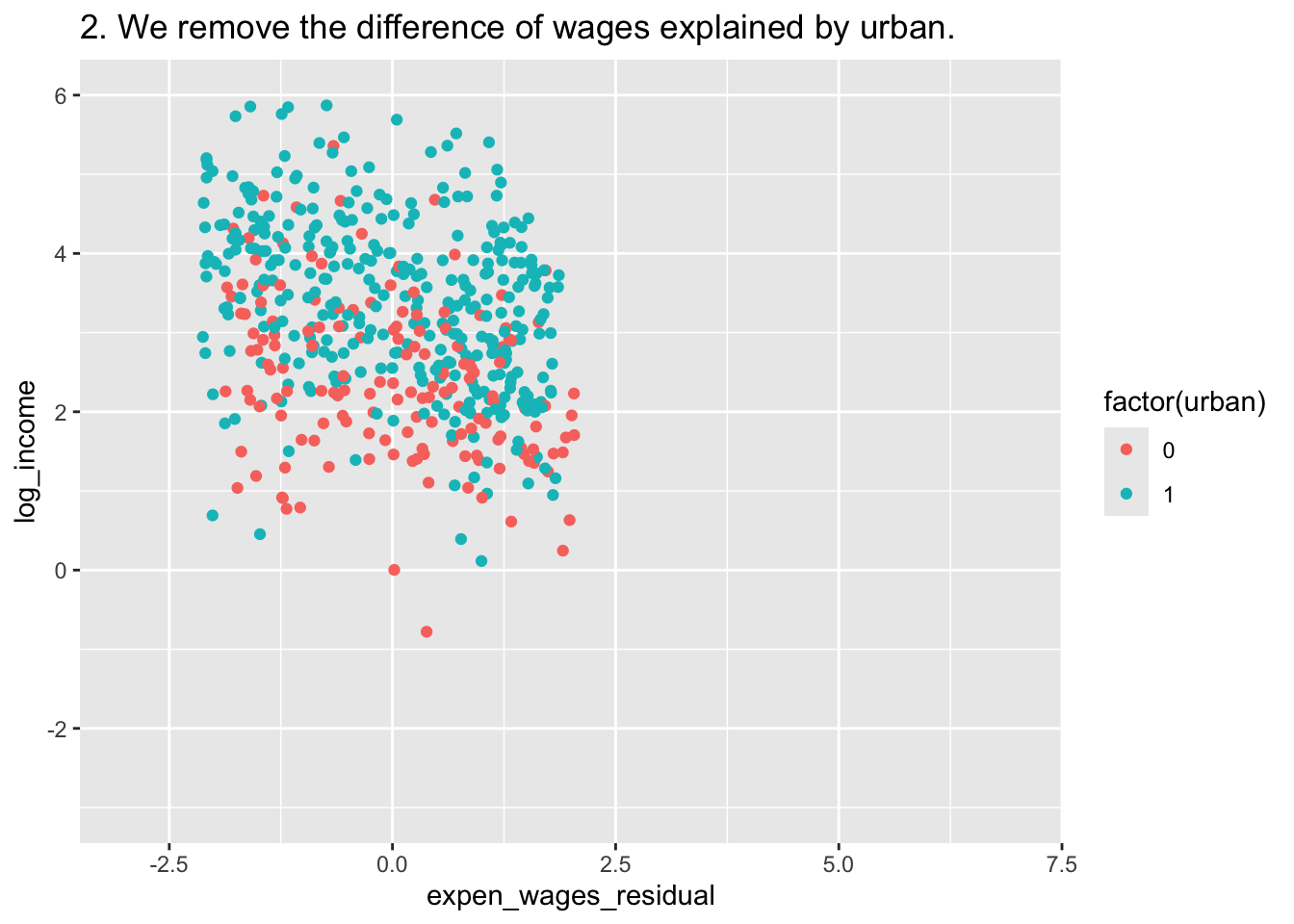

D <- ggplot(df, aes(x=expen_wages_residual,y=log_income_residual,color = factor(urban))) +
  geom_point() +
  labs(title = "3. We remove the difference of income explained by urban.")+
  xlim(c(-3,7)) + ylim(c(-3,6))
D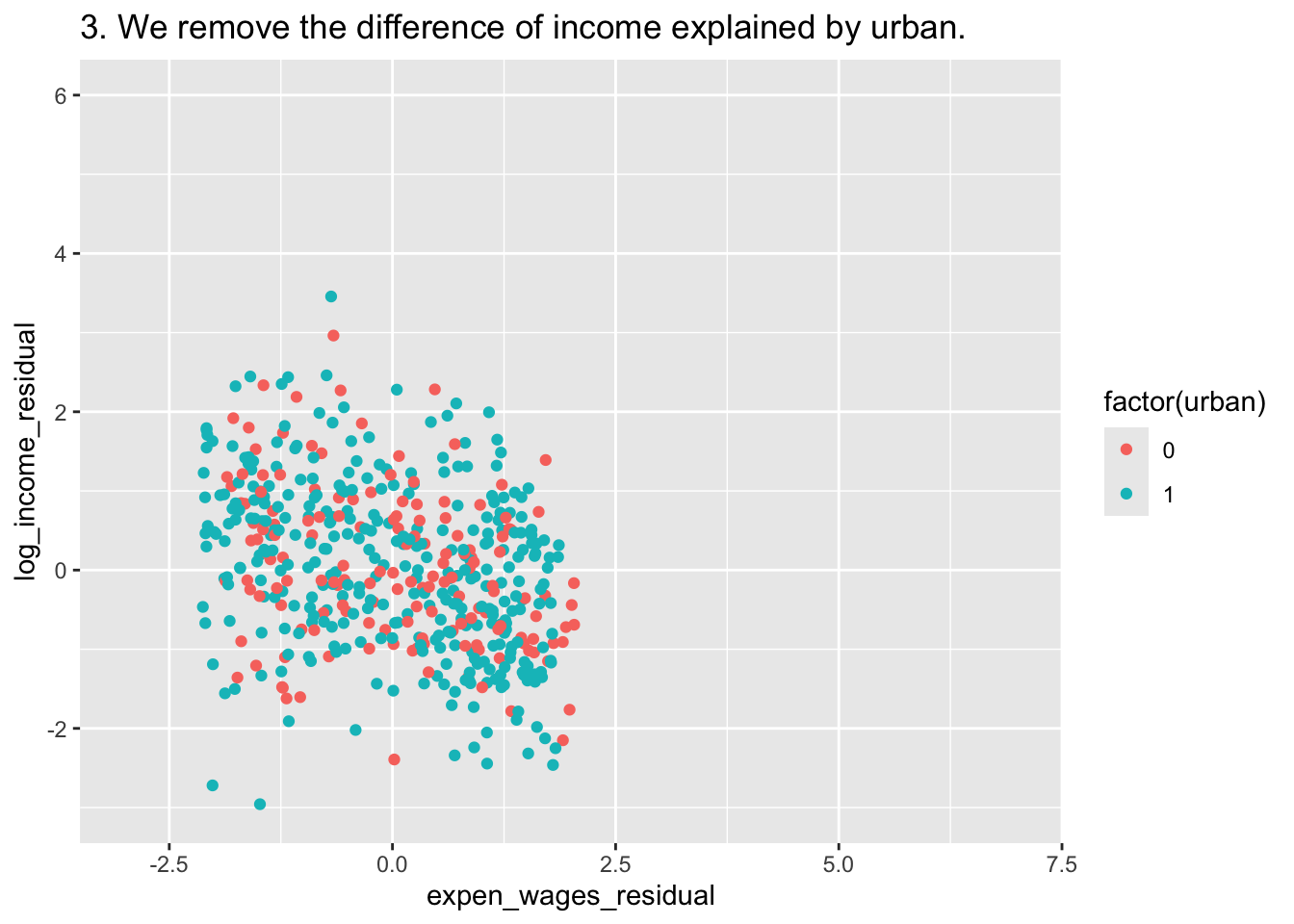

E <- ggplot(df, aes(expen_wages_residual,y=log_income_residual)) +
  geom_point() +
  labs(title = "4. We analize what is left. Beta = -0.22") +
  geom_smooth(method = "lm")+
  xlim(c(-3,7)) + ylim(c(-3,6))
E

## `geom_smooth()` using formula = 'y ~ x'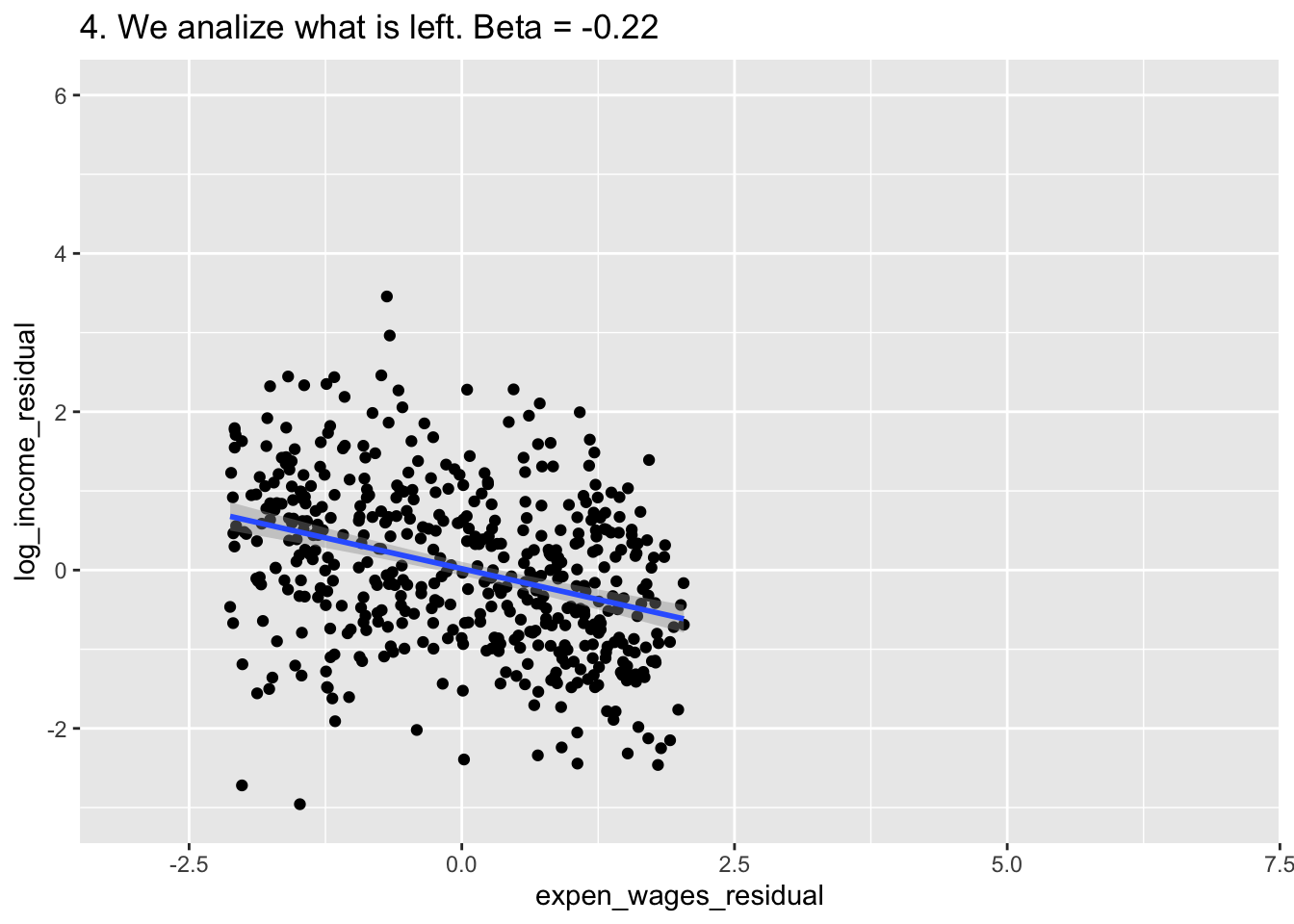

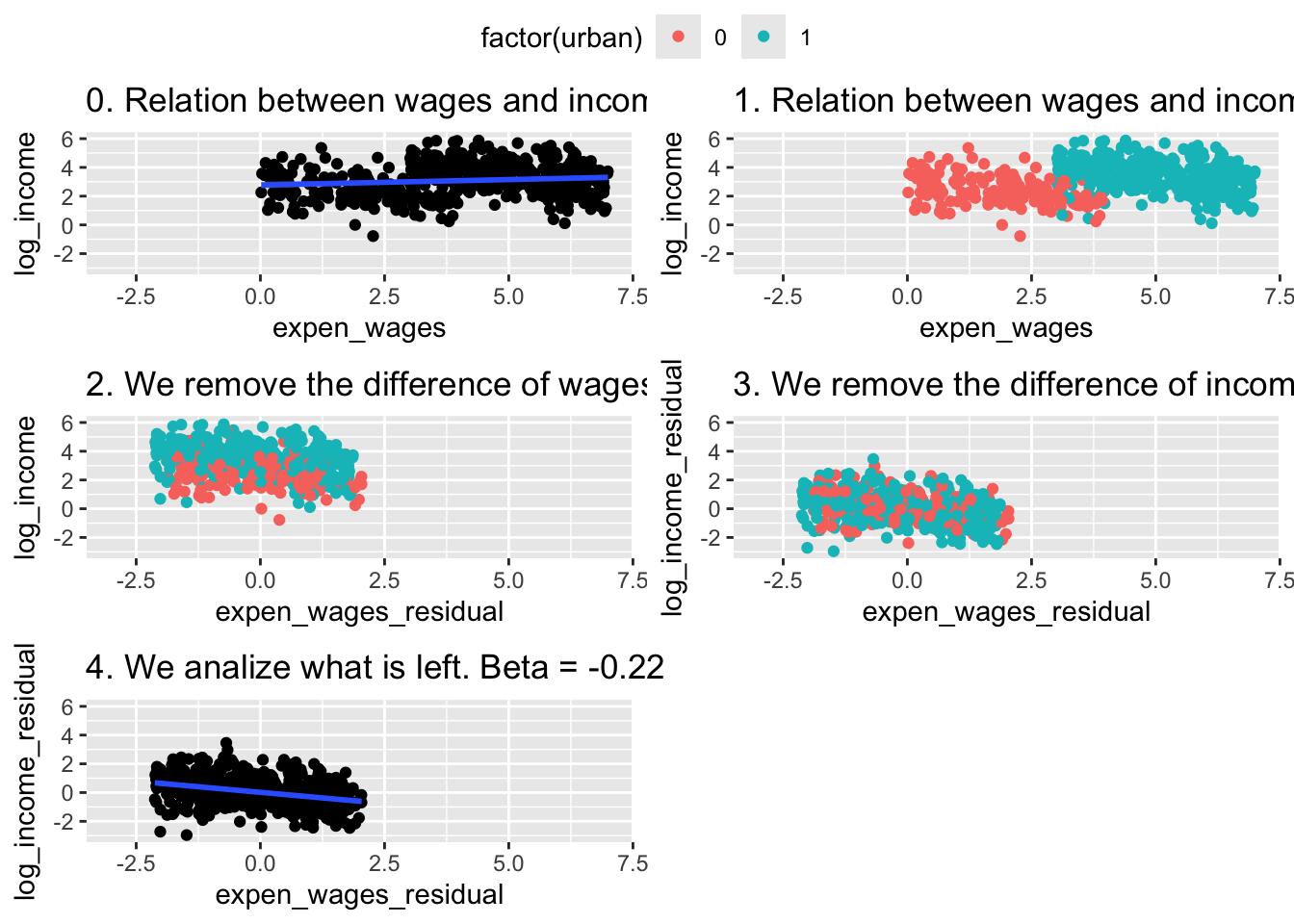
ggarrange(A,B,C,D,E,
          common.legend = T,
          ncol = 2,
          nrow = 3)

## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'